
KSSOLV
2.支持Windows、IOS和Linux等操作系统
3.支持GPU加速
4.拥有可视化界面

KSSOLV是一套采用MATLAB语言编写、支持GPU加速、能实现基础科研与教学一体化的轻量化赝势平面波电子结构软件工具集。KSSOLV能够进行基态及激发态电子结构、杂化泛函、结构优化等计算,具有强大的可视化功能、热点分析功能,致力于促进发展量子力学的科普教育以及帮助研究者开发新算法。

KSSOLV(Kohn-Sham Solver)是一款基于平面波基组的求解Kohn-Sham密度泛函理论的软件,采用MATLAB语言编写,类似Python为解释型语言,易于读写,可降低学习成本。KSSOLV无需额外编译安装,支持Windows、Mac OS X和Linux系统。其中KSSOLV-GPU是KSSOLV的英伟达GPU加速版本。
KSSOLV-GPU通过GPU加速后,可快速求解第一性原理密度泛函理论KS方程,且无需安装即可运行。KSSOLV-GPU加速后在个人PC端可达到主流计算软件的速度,这使课堂上演示量子力学计算成为可能。KSSOLV是一套既可以代替主流计算软件科研,又适用于教学的科教一体化计算程序,可以应用到前沿交叉科学研究和教学中。
第一性原理计算软件综合了数学、物理和化学理论知识的代码实现,可以搭建起理论与实验之间的桥梁,能帮助学生更好地整理自己的知识体系。因此,高校物理化学专业的本科生或低年级研究生,在步入科研生涯之前或开展科研之初很有必要学习第一性原理计算的理论以及相关的软件。然而,如果将第一性原理计算程序搬入课堂,教授学生使用计算软件的门槛高,难度大。

薛定谔方程
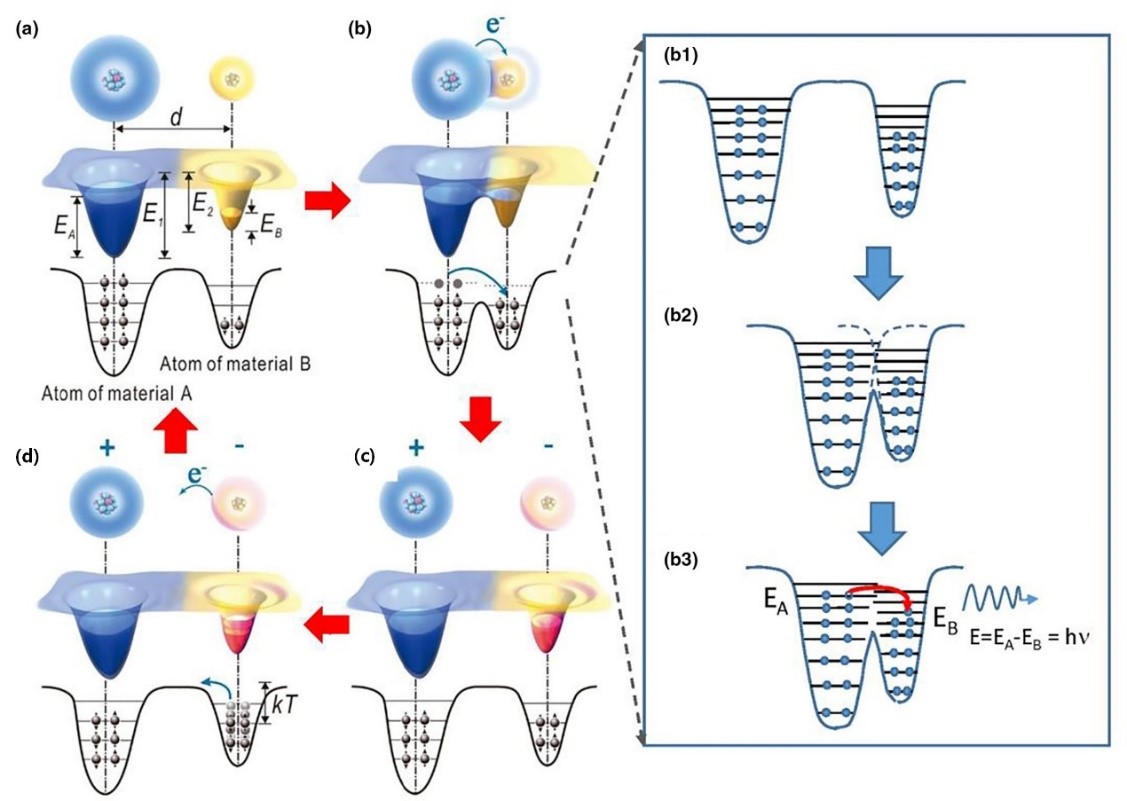
微观电子相互作用模型
放眼当前国内市场,占主流地位的是欧美等国外计算软件。它们大多采用Fortran/C++编写,不易理解,多数软件不支持在个人PC的WINDOWS环境下运行,这不利于将第一性原理计算程序搬入课堂进行教学演示。KSSOLV-GPU采用解释性语言MATLAB语言编写,学习成本较较低,易于读写,无需编译即可在个人PC的WINDOWS操作系统下快速运行,再加上便捷的可视化界面,让第一性原理软件在课堂上演示成为现实,可以填补国内第一性原理计算教学软件的空白。同时,借助KSSOLV-GPU平台还可以开展项目式和仿真式相结合的教学模从而给本科生、研究生量子力学的创新型教学提供有力的平台,培养学生的计算思维和并行计算能力,为以后专业课学习和科研能力的培养打下扎实的计算基础。
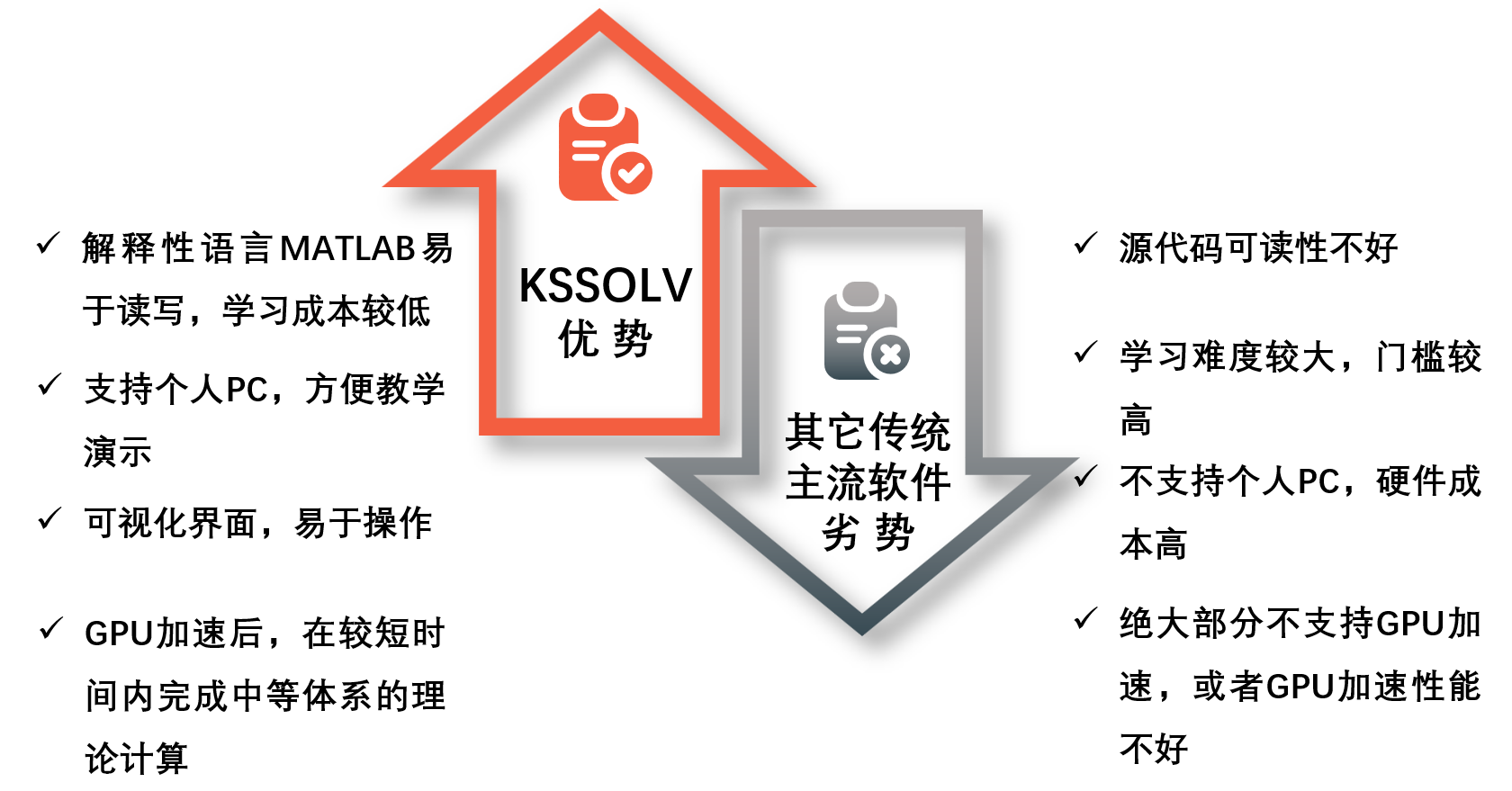
除了教学以外,KSSOLV-GPU也能成为科研人员可行可用的第一性原理计算工具。KSSOLV编程语言简单,入门门槛低,但是又拥有科研级的计算精度,因此可助力科研人员研究量子力学。对于第一性原理计算的算法开发者,KSSOLV-GPU具有其他软件所没有的优势。

KSSLOV利用密度泛函理论近似求解薛定谔方程得到能量、原子力等信息,能够使用局域密度近似(LDA)、广义梯度近似(GGA)、杂化泛函(HSE06)近似等方法求解Kohn-Sham方程。KSSLOV能利用MATLAB的GPU加速工具进行GPU加速,其能够采用GPU加速的计算功能包括:

作为一款轻量化赝势平面波电子结构软件,KSSOLV拥有自己独特的优势,尤其是可在Windows、Mac OS X系统上运行,在目前市场上是独一无二的。
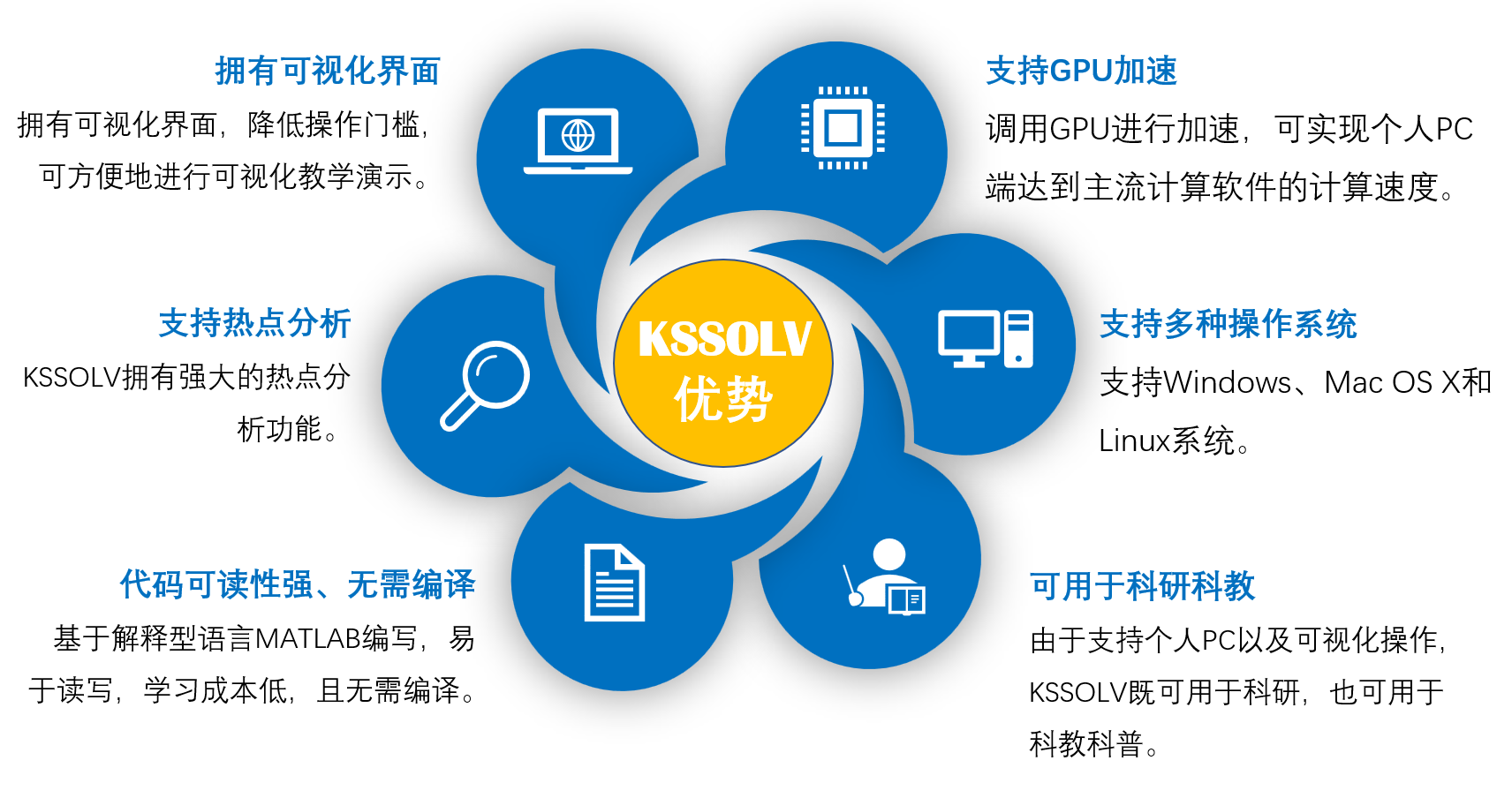
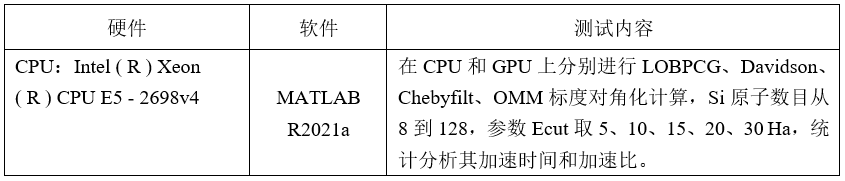
KSSOLV是一套采用MATLAB语言编写、基于平面波基组来求解Kohn - Sham密度泛函理论( DFT )问题的软件工具集。在DFT计算中,最昂贵的部分通常是自洽场( SCF )中Kohn - Sham哈密顿量的对角化。为了使个人电脑能够进行中等规模(约百原子)的DFT计算,我们利用MATLAB内置的并行计算工具箱,提出了一种CPU-GPU混合方法,以加速KSSOLV中的迭代对角化算法。我们将KSSOLV-GPU在RTX3090、V100、A100三种GPU上的性能与KSSOLV在常规CPU上的性能进行比较。
测试内容
在RTX3090、V100和A100三种不同类型的GPU上测试了矩阵乘法( mtimes)、快速傅里叶变换( fft )、元素积(times)、水平级联( horzcat )、矩阵除法( mrdivide )和特征值( eig )的性能,并与MATLAB中的CPU进行了比较,用加速比来表示每个GPU的加速能力。
测试条件

测试结果

表 4-1-1 选取矩阵乘法( mtimes)、快速傅里叶变换( fft )、元素乘积(times)、水平级联( horzcat )、矩阵除法( mrdivide )和特征值( eig ) MATLAB运算在测试矩阵全维上的最大GPU加速比。加速比由CPU的运算时间除以GPU运算时间得到。

图 4-1-1 ( a )矩阵乘法( mtimes)、( b )快速傅里叶变换( fft )、( c )元素乘积(times)、( d )水平级联( horzcat )、( e )矩阵除法(mrdivide )和( f )特征值( eig )随测试矩阵维数增加,在MATLAB上,三种不同类型的GPU上分别与CPU的运算性能进行比较。
可以看到,不同的操作在GPU上都有相当大的加速比。对于V100和RTX3090 GPU,RTX3090作为最新的消费级GPU在eig、horzcat和times操作上的性能与V100相当甚至更好,但在fft上的性能只是V100的一半,在mtimes 和 mrdivide操作上的性能分别是V100的1/10和1 /5左右。因此,可以在此基础上推断出对KSSOLV迭代对角化算法GPU加速性能良好。
测试内容
测试随Si原子数的增加,在CPU和GPU上相同算法的计算性能和扩展性。
测试条件
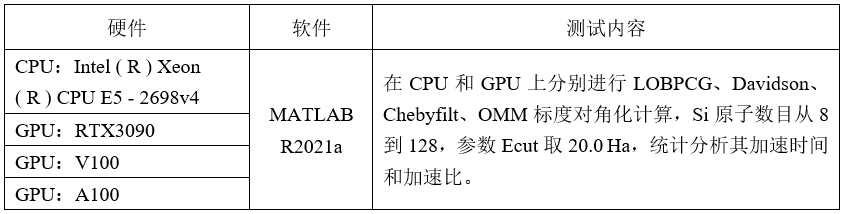
测试结果

图4-2-1 取Ecut = 20.0Ha,在CPU和GPU上进行不同的对角化运算,时间消耗随着Si原子数目的增加而增加。(a)在CPU和GPU上进行LOBPCG对角化计算;(b)在CPU和GPU上进行Davidson对角化计算;(c)在CPU和GPU上进行Chebyfilt对角化计算;(d)在CPU和GPU上进行OMM对角化计算。
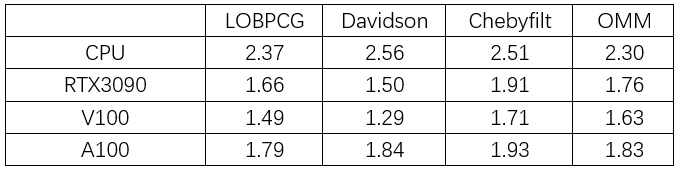
表4-2-1 取Ecut = 20.0Ha,在CPU、RTX3090、V100和A100上分别对LOBPCG、Davidson、Chebyfilt和OMM对角化算法的散点图进行线性拟合得到标度。
在不同GPU上测试了不同算法的加速比,结果如图4-2-2所示。加速比(speedup ratio)的计算公式为:
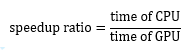
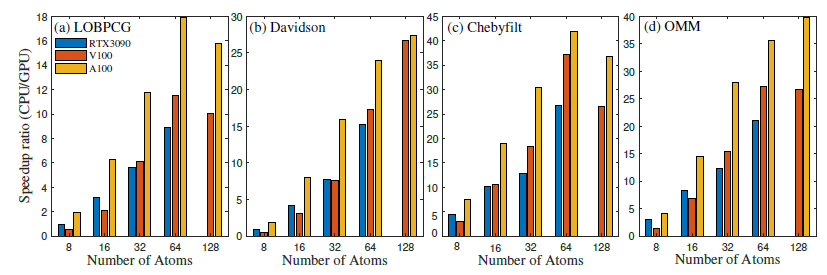
图4-2-2 取Ecut = 20.0Ha,与CPU相比,通过GPU加速后,不同对角化算法的加速比随着Si原子数目的增加而增大;(a)LOBPCG在不同GPU上的加速比;(b) Davidson在不同GPU上的加速比;(c) Chebyfilt在不同GPU上的加速比;(d)OMM在不同GPU上的加速比。

表4-2-2 LOBPCG、Davidson, Chebyfilt和OMM对角化算法在RTX3090、 V100和A100 上的最大加速比
从测试的结果可以发现,所有对角化算法的执行时间随着原子数目的增加而变长,GPU的加速效果明显。通过GPU加速,可以降低对角化过程的标度,通过GPU进行多线程并行计算,使得计算过程更快。
测试内容
测试随Si原子数的增加,且选取不同Ecut值时,在CPU和GPU上相同算法的计算性能和扩展性。
测试条件
测试结果
(1)LOBPCG
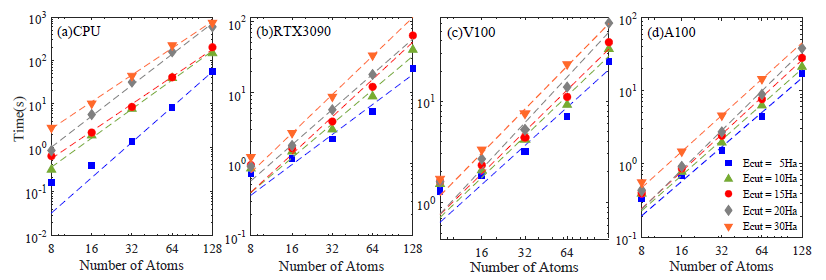
图4-3-1 取不同的Ecut、在不同的CPU、CPU下,LOBPCG的时间消耗随着原子数目增加的变化:( a )通过CPU进行LOBPCG对角化计算;( b)通过RTX3090进行LOBPCG对角化计算;( c )通过V100进行LOBPCG对角化计算;( d )通过A100进行LOBPCG对角化计算。
(2)Davidson
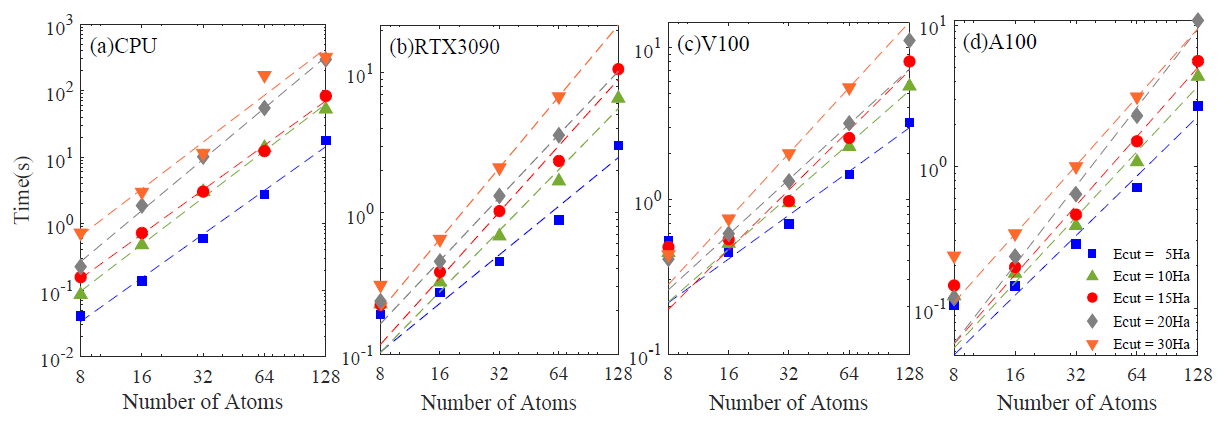
图4-3-2 取不同的Ecut、在不同的CPU、CPU下,Davidson的时间消耗随着原子数目增加的变化:( a )通过CPU进行Davidson对角化计算;( b)通过RTX3090进行Davidson对角化计算;( c )通过V100进行Davidson对角化计算;( d )通过A100进行Davidson对角化计算。
(3)Chebyfilt
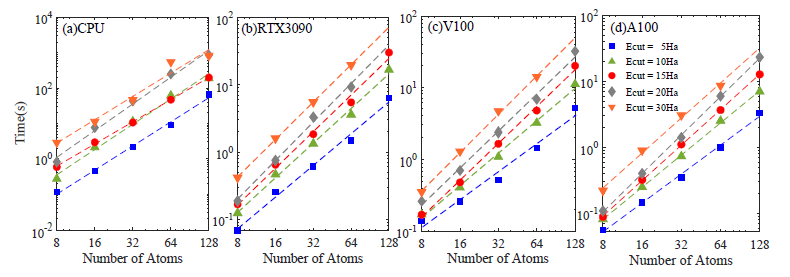
图 4-3-3 取不同的Ecut、在不同的CPU、CPU下,Chebyfilt的时间消耗随着原子数目增加的变化:( a )通过CPU进行Chebyfilt对角化计算;( b)通过RTX3090进行Chebyfilt对角化计算;( c )通过V100进行Chebyfilt对角化计算;( d )通过A100进行Chebyfilt对角化计算
(4)OMM
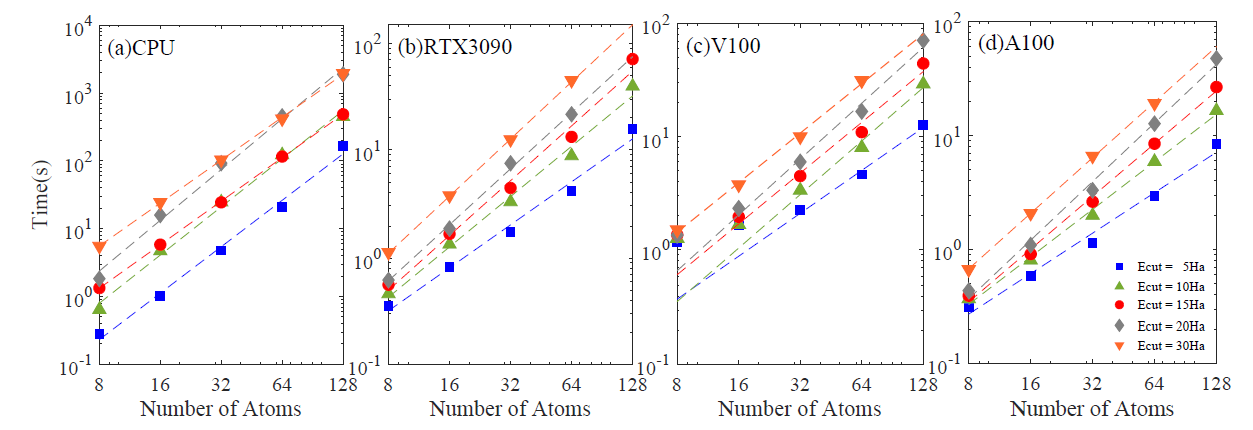
图4-3-4 取不同的Ecut、在不同的CPU、CPU下,OMM的时间消耗随着原子数目增加的变化:(a)通过CPU进行OMM对角化计算;(b)通过RTX3090进行OMM对角化计算;(c)通过V100进行OMM对角化计算;(d)通过A100进行OMM对角化计算。
计算结果

表4-3-1 不同对角化算法在不同Ecut的CPU和GPU上的标度测试结论
通过在CPU和GPU上测试不同对角化算法的标度和加速比,与基于CPU计算相比,GPU拥有强大的加速性能和更低的基态计算规模。尤其是性价比较好的最新消费级GPU卡RTX3090,其计算性能不输于数据中心级V100,充分说明可以借助MATLAB强大的可视化能力和优秀的消费级GPU卡来实现KSSOLV-GPU的加速计算和可视化,从而得以在个人电脑上快速完成第一性原理计算和可视化分析,降低计算材料科学的门槛。
应用一:KSSOLV助力氮化镓(GaN)半导体p-n异质结中实现独特的光电流极性反转(即双向光电流现象)
2021年,中国科学技术大学微电子学院龙世兵教授、孙海定研究员团队在氮化镓(GaN)半导体p-n异质结中实现了独特的光电流极性反转(即双向光电流现象)。相关成果以“Bidirectional photocurrent in p–n heterojunction nanowires”为题于9月23日发表在《自然 电子学》上(Nature Electronics 2021, 4, 645–652)。这是中国科大首次以第一作者单位在电子器件领域知名期刊Nature Electronics上发表研究论文。中科大研究员、瀚海量子创始人胡伟参与了该项目的联合攻关,利用团队的KSSOLV软件帮助作者完成论文中的DFT理论计算部分。
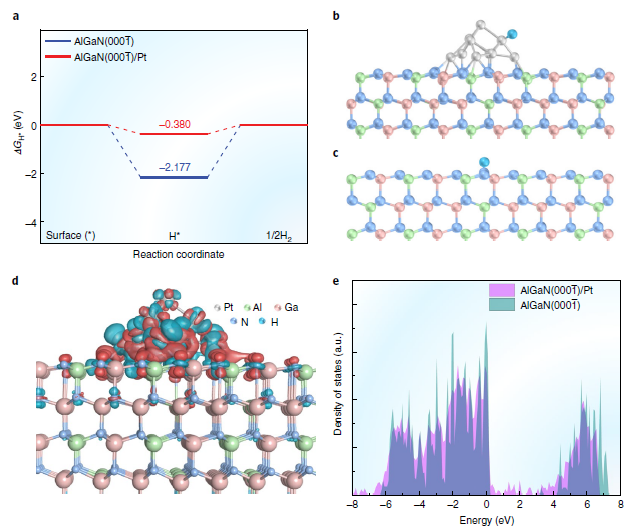
Danhao Wang, Xin Liu, Yang Kang, Xiaoning Wang, Yuanpeng Wu, Shi Fang, Huabin Yu,Muhammad Hunain Memon, Haochen Zhang, Wei Hu, Zetian Mi, Lan Fu, Haiding Sun*,Shibing Long, Bidirectional photocurrent in p–n heterojunction nanowires,Nat. Electron.4(9), 645-652, (2021).
应用二:KSSOLV助力光解水催化剂理论设计
2021年,中国科学技术大学杨金龙课题组胡伟研究团队高蕴智博士在国际学术期刊JPCL上发表了论文,在论文中提供了一种基于边界修饰纳米带的通用策略以设计Z-scheme异质结水分解光催化剂。值得注意的是,高博士在研究过程中,使用了课题组自主研发的第一性原理计算软件KSSOLV实现了线性响应含时密度泛函理论LR-TDDFT计算,大大加快了研发进度。

Yunzhi Gao, Cenfeng Fu, Wei Hu*, and Jinlong Yang*, J. Phys. Chem. Lett. 2022, 13, 1, 1–11
得益于可在个人PC上运行的独特优势,再加上可视化的操作界面,KSSOLV使得在课堂上为学生演示量子力学计算过程成为可能。又由于第一性原理软件的开发与学习过程中涵盖了数学、物理、化学、计算机四大基础学科,KSSOLV可助力深化高校基础学科建设,培养交叉学科复合型人才。同时,作为一款科研级第一性原理计算软件,科研工作者也快速、方便地利用KSSOLV进行量子力学领域研究。

[1] 插值可分密度拟合分解加速线性响应时变密度泛函理论计算分子和固体的激发能
Wei Hu, Jie Liu*, Yingzhou Li, Zijing Ding, Chao Yang, and Jinlong Yang*, Accelerating excitation energy computation in molecules and solids within linear-response time-dependent density functional theory via interpolative separable density fitting decomposition, J. Chem. Theory Comput.16:964-973, (2020).
[2] 线性响应时变密度的两级迭代求解器
Jie Liu, Wei Hu, Jinlong Yang*, Two-level iterative solver for linear response time-dependent density functional theory with plane wave basis set, J. Chem. Phys. 154(6): 064101, (2021).
[3]加速自洽场迭代的椭圆预调节器
Accelerating Optical Absorption Spectra and Exciton Energy Computation via Interpolative Separable Density Fitting, Wei Hu, Meiyue Shao, Andrea Cepellotti, Felipe H.da Jornada, Lin Lin, Kyle Thicke, Chao Yang*, Steven G. Louie, ICCS, 2018, 10861, 604-617.
[4] 正交约束优化问题的交替梯度法
Yanmei Sun, Yakui Huang*, An alternate gradient method for optimization problems with orthogonality constraints,Numer. Algebra, Control. Optim.11(4): 665-676, (2021).
[5]G0W0中的低秩分解
MeiYue Shao, Lin Lin, Chao Yang*, Fang Liu, Felipe H. Da Jornada, Jack Deslippe & Steven G. Louie , Low rank approximation in G 0 W 0 calculations,Sci. China Math.59:1593–1612 (2016)
[6]在GW近似下从头计算多电子自能的数值积分
Fang Liu*, Lin Lin, Derek Vigil-Fowler, et al. ,Numerical integration for ab initio many-electron self energy calculations within the GW approximation. J. Comput. Phys. 286: 1-13 (2015).
[7]电子排斥积分张量的超收缩格式的压缩
Jianfeng Lu*,Lexing Ying,Compression of the electron repulsion integral tensor in tensor hypercontraction format with cubic scaling cost, J. Comput. Phys. 302: 329-335, (2015).
[8] 广义戴维森算法的网格独立性
C.T.Kelley*,J.Bernholc, et al. ,Mesh independence of the generalized Davidson algorithm, J. Comput. Phys. 409: 109322, (2020).
[9]正交约束优化问题的结构拟牛顿方法
Jiang Hu*, Bo Jiang, Lin Lin, Zaiwen Wen, and Ya-xiang Yuan,Structured quasi-Newton methods for optimization with orthogonality constraints, SIAM J. Sci. Comput. 41(4),(2019).
[10]使用间断伽辽金算法的量子模拟
Jarrod R McClean , Fabian M Faulstich, Qinyi Zhu, et al. Discontinuous Galerkin discretization for quantum simulation of chemistry, New. J. Phys. 22, 093015, (2020).
[11]KohnSham平面波离散后的后处理
Cancès E, Dusson G, Maday Y, et al. A perturbation-method-based post-processing for the planewave discretization of Kohn–Sham models, J. Comput. Phys.307: 446-459, (2016).
[12]大规模特征空间计算中的迹最小化
Zaiwen Wen*, Chao Yang, Xin Liu ,Yin Zhang, Trace-penalty minimization for large-scale eigenspace computation, J. Sci. Comput., 66:1175-1203, (2016).
[13]精确Hessian自适应正则化自洽场迭代法用于电子结构计算
Zaiwen Wen, Andre Milzarek, Michael Ulbrich, Hongchao Zhang, Adaptive regularized self-consistent field iteration with exact Hessian for electronic structure calculation, SIAM J. Sci. Comput. 35(3), (2013).
[14]系综密度泛函理论的近端梯度法
Michael Ulbrich, Zaiwen Wen, Chao Yang, Dennis Klöckner, Zhaosong Lu, A proximal gradient method for ensemble density functional theory, SIAM J. Sci. Comput. 37(4),(2015).
[15] p-n异质结纳米线的双向光电流
Danhao Wang, Xin Liu, Yang Kang, et al., Bidirectional photocurrent in p–n heterojunction nanowires,Nat. Electron. 4(9), 645-652, (2021).
[16] 利用边缘修饰的磷烯纳米带设计直接z型异质结用于光催化整体水分离
Yunzhi Gao, Cenfeng Fu, Wei Hu*, and Jinlong Yang*, Designing Direct Z-Scheme Heterojunctions Enabled by Edge-Modified Phosphorene Nanoribbons for Photocatalytic Overall Water Splitting, J Phys. Chem. Lett. 13: 1-11, (2021).


